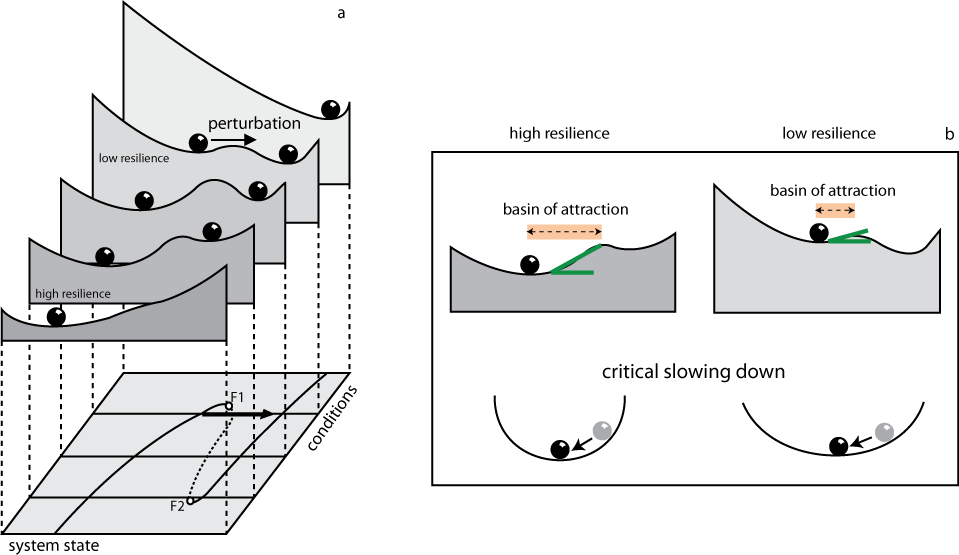
A simple way to understand why we should expect early warnings before critical transitions is to think of the behavior of a system as the motion of a ball in a landscape of valleys and hilltops (panel a). Balls represent the state of the system. Valleys correspond to  the basins of attraction of the two alternative stable states of the system. The width and the steepness of the basin of attraction determine the capacity of the system to absorb a perturbation without shifting to an alternative state, and reflects the resilience of the state of the system. As conditions bring the system close to a critical transition (critical threshold1), the basin of attraction of the current state of the system shrinks and so does its resilience: even a tiny perturbation is enough to shift the sphere to the alternative valley. At the same time, the steepness of the basin of attraction becomes lower: this means that the same perturbation that may not tip the system, it will definitely take longer to dissipate due to the phenomenon of critical slowing down (panels b, c). Mathematically, critical slowing down is connected to the fact that close to the critical transition the dominant eigenvalue of the system at equilibrium vanishes. Practically, critical slowing down enables us to probe the dynamics of the system in order to assess its resilience and the risk of an upcoming transition.