Basics
Conditional heteroskedasticity means that variance at one time step has a positive relationship with variance at one or more previous time steps. This implies that periods of high variability will tend to follow periods of high variability and periods of low variability will tend to follow periods of low variability. As variability tends to increase prior to a transition, conditional heteroskedasticity can serve as a leading indicator because the portion of a time series near an impending shift will appear as a cluster of high variability while the portion of the time series away from the shift will appear as a cluster of low variability. Conditional heteroskedasticity is based on a Langrange multiplier test, which is calculated by first extracting the residuals of a fitted model to the time series. Usually an autoregressive model of selected order is selected according to a measure of relative goodness of fit (e.g. the Akaike Information Criterion); then the residuals are squared, and finally the residuals are regressed on themselves lagged by one time step. A positive slope of the linear regression of the lagged residuals suggests conditional heteroskedasticity. The coefficient of determination of the regression r2 is compared with a χ2 distribution of one degree of freedom to assign the significance for the r2. The χ2 value can be divided by the sample size to make it directly comparable to the r2 value.
Example
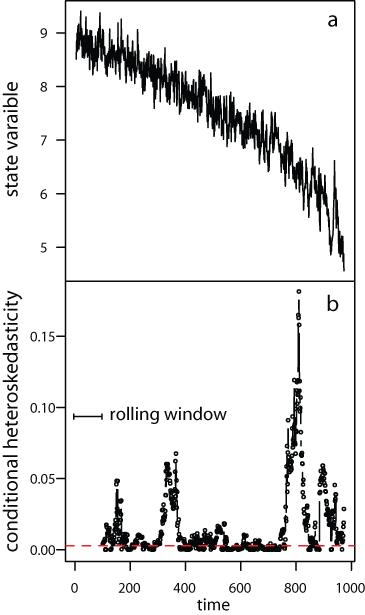
We present the CH method applied to a simulated time series in which a critical transition is approaching (panel a). Conditional heteroskedasticity (CH) was estimated in rolling windows of 10% the size of the time series. Within each rolling window we fit an autoregressive model selected using AIC from a suite of AR(p) models applied to the original data. Although measurement and process error remained constant in our example, we chose a relatively small rolling window size to minimize the chance of estimating an artificially large CH caused by increasing noise along the time series. We found significant CH (at P=0.1), which became consistently significant at the last part of the record (close to the transition) (panel b).