Basics
Threshold AR(p) models are not, strictly speaking, early warnings for critical transitions. They constitute, however, a method that is suitable for detecting flickering just like potential analysis does. Flickering occurs when a time series repeatedly crosses the domains of attraction of two alternative states. Flickering detection methods can robustly indicate the presence of alternative regimes during the period that the system has not permanently shifted to the alternative attractor, and, thus, serve as an early warning for a permanent shift to an alternative state.
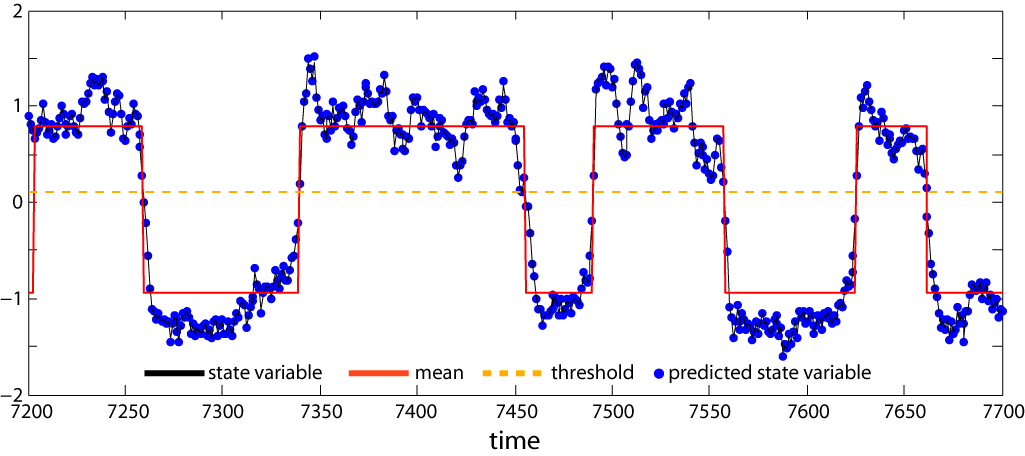
The difficulty in identifying flickering lies in robustly estimating that a time series is jumping among two (or more) distinct states. Threshold AR(p) models are designed to identify these occasional transitions. These models assume there are two underlying processes governing the dynamics in a time series, with the possibility that the state variable switches between them when it crosses a threshold. The two processes are described by two AR(p) models. As with the time-varying AR(p) models, we can also incorporate measurement error, and use the Kalman filter to compute likelihoods that can be used for parameter estimation and model selection.
Example
We fitted the threshold AR(p) model to a time series that does approach a critical transition, but nonetheless under a strong stochastic regime that caused the the time series to jump between multiple states (panel a). The threshold AR(p) model was applied on log-transformed and standardized data. Assuming that the time series was produced by two AR(p) processes of the same order, we fitted AR(p) models of order 1, 2, and 3 and found that the best-fitting model was an AR(3). The fitted threshold AR(p) models showed that the dataset was characterized by two distinct states, which suggested that the system would eventually stabilize in the alternative state.