Basics

Often we do not know the underlying processes that generate the time series that we are analyzing for early warnings. Nonparametric drift-diffusion-jump (DDJ) models address this problem by fitting a general model that can approximate a wide range of nonlinear processes without the need to specify an explicit equation. Drift measures the local rate of change. Diffusion measures relatively small shocks that occur at each time step. Jumps are large intermittent shocks. Total variance combines the contributions of diffusion and jumps. The approach is to estimate terms of a drift-diffusion-jump model as a surrogate for the unknown data generating process.

From a time series we can estimate drift, diffusion and jump statistics that may serve as leading indicators of the transition. We do this by assuming that high-frequency observations of the system can be approximated by fitting a drift-diffusion-jump model:

dx(t) = f(x(t),θ(t))dt + g(x(t), θ(t))dW + dJ(t)

In this fitted model, the drift function f(.) measures the instantaneous deterministic change in the time series, the diffusion function g(.) measures the standard deviation of relatively small shocks that occur at each time step, whereas jumps J, the last term, are relatively large shocks that occur intermittently. In practice, the drift, diffusion, and jump functions are estimated using nonparametric regression. The regression yields estimates of drift, total variance, jump intensity, and diffusion variance. In addition, we can estimate conditional variance of x using standard nonparametric regression techniques. This conditional variance rises to infinity at the critical transition.

An interesting feature of the drift-diffusion-jump model is that conditional variance and diffusion estimates may be useful for distinguishing bifurcations that occur in the drift from bifurcations that occur in the diffusion (so-called noise-induced transitions: an abrupt shift in the shape of the stationary distribution). A bifurcation in the drift only may be indicated in advance by conditional variance but not diffusion. A bifurcation in the diffusion may be indicated by increases in both conditional variance and diffusion.

Example

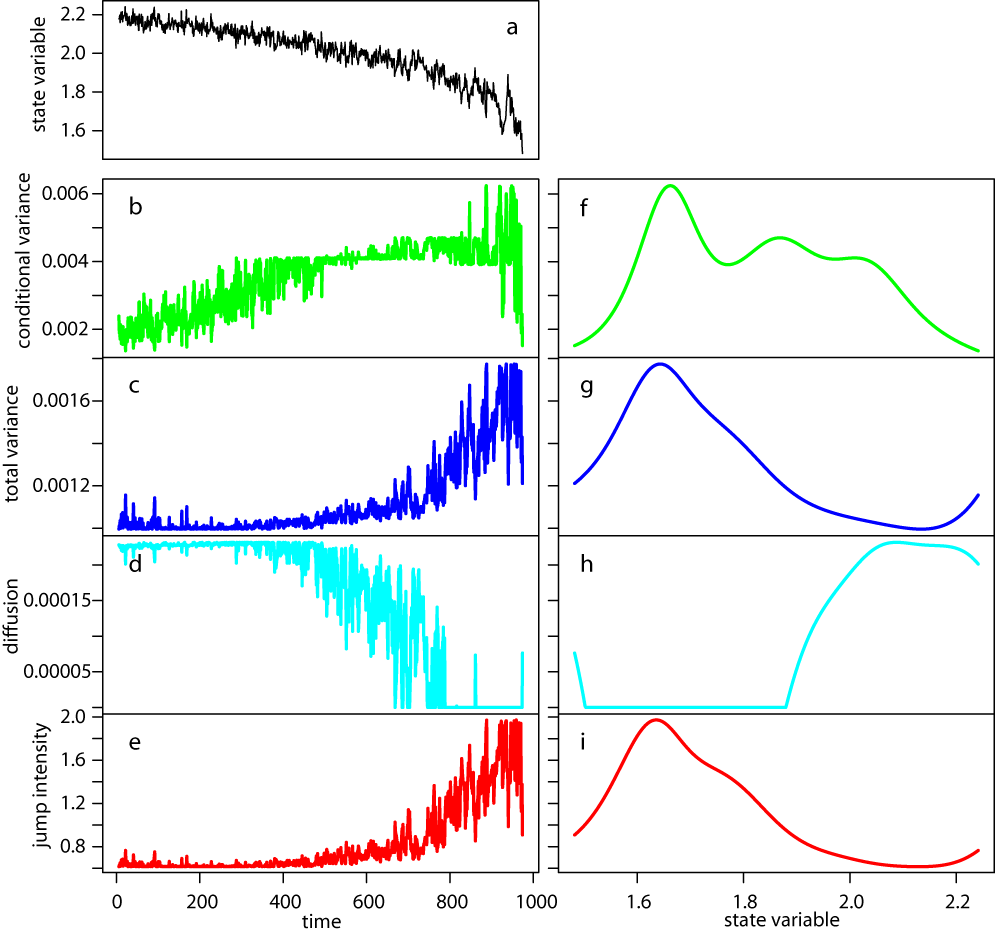
We present the DDJ method applied to a simulated time series in which a critical transition is approaching. The nonparametric DDJ model was not applied on rolling windows, but to the entire time series after log-transforming the data (panel a). We found an increase in conditional and total variance as well as in jump intensity in the time series (panels b, c, e) and a decrease in the diffusion term (panel d). The trends were noisy, but they became very clear when plotted against biomass values (due to smoothing) (panels f-i). For log-transformed values between 1.6 and 1.8, the indicators started to signal the upcoming transition.