The simplest way to measure the approach to a potential tipping point would be to directly measure the recovery time (or rate) of the state of the system back to its initial equilibrium state following a perturbation. In case the system is close to a tipping point the recovery time should increase (or the recovery rate should decrease). This is the essence of critical slowing down.

 

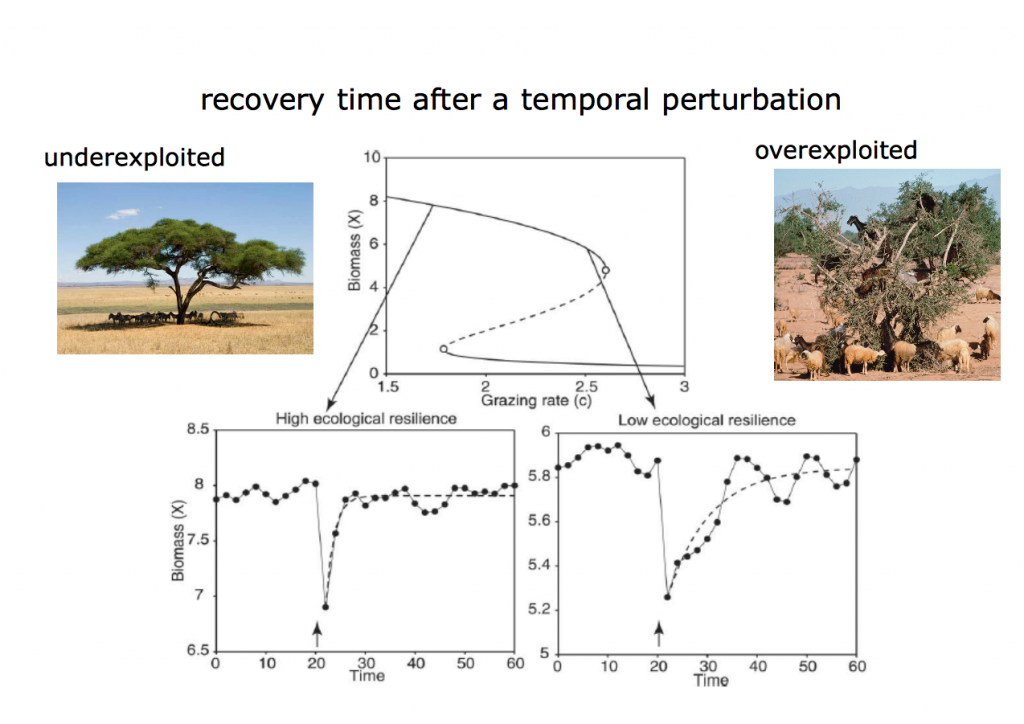
Indeed, it has been shown that performing a perturbation (pulse) experiment in a situation where a system is far from a transition (fig.1 low left panel) and in a case that is close to a transition (fig.1 low right panel), one could clearly see the difference in the time that it takes for the system to return back to its initial equilibrium state. The longer that time is, the less stable the system and thus more close to a potential tipping point (fig.1 top panel). In this virtual experiment,  one compares directly the recovery time by standardizing the size of the perturbation: removing the same 10% of the standing biomass of the simulated resource allows for the direct comparison of recovery time. This is important as it is obvious that a stronger perturbation takes longer to recover, thus no conclusion on the proximity to a tipping point can be easily made.  In a real case experiment, recovery time might be difficult to use to compare systems or instances of a system. In such situations using recovery rate is a better indicator.

 

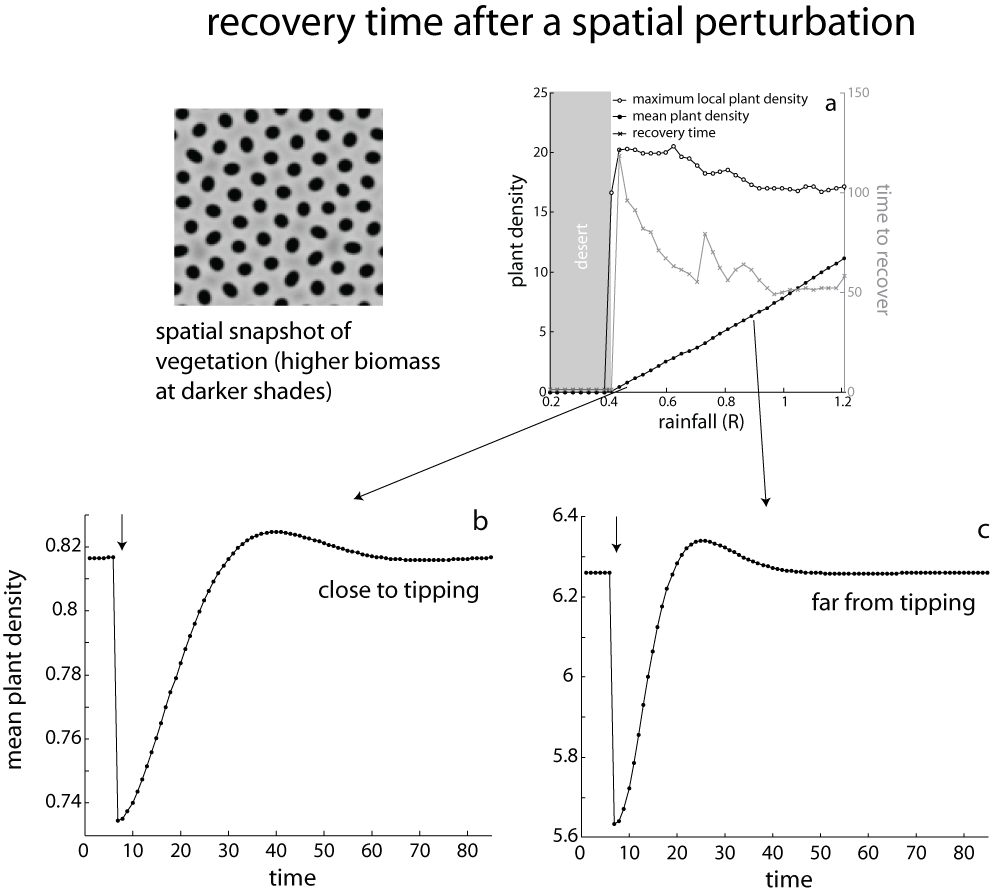
The above numerical experiment was conducted on a simple example where one could be able to remove (perturb) part of the resource (state variable) in an environment where the whole resource could be thought of as one entity both to measure and to manipulate (a homogeneous case). In a more realistic scenario, one could think of a system expanding in space. A similar perturbation experiment can be conducted by removing a resource that grows in space (a square lattice, fig2). In this case by removing 10% of the resource biomass everywhere in space and measuring the time it takes for the system to recover back to equilibrium (fig2 panels b, c), we find a similar result as in fig.1. In other words, critical slowing down works in space as well and we can measure it with a similar perturbation experiment!

 

Perturbation experiments are the most straightforward way to measure critical slowing down. In some cases they can be more informative than other early-warning signals, which may even fail to announce an approaching transition (see Dakos et al 2011). However they may be difficult to conduct both for practical and conceptual reasons. Not only it is difficult to remove a part of biomass of a population, but such perturbation may potentially trigger itself a transition in case it pushes the state of the system beyond its present basin of attraction.