Basics

The BDS test (after the initials of W. A. Brock, W. Dechert and J. Scheinkman) detects nonlinear serial dependence in time series. The BDS test was not developed as a leading indicator, but it can help to avoid false detections of critical transitions due to model misspecification. After detrending (or first-differencing) to remove linear structure from the time series by fitting any linear model (e.g. ARMA(p,q), ARCH(q) or GARCH(p,q) models), the BDS tests the null hypothesis that the remaining residuals are independent and identically distributed (i.i.d.). Rejection of the i.i.d. hypothesis implies that there is remaining structure in the time series, which could include a hidden nonlinearity, hidden nonstationarity or other type of structure missed by detrending or model fitting. As critical transitions are considered to be triggered by strong nonlinear responses, the BDS test is expected to reject the i.i.d. hypothesis in the residual time series from a system that is approaching a critical transition. The BDS test can be helpful as an ad-hoc diagnostic test to detect nonlinearities in time series prior to transitions: if the BDS test rejects the i.i.d. hypothesis and there is another strong leading indicator, then the detected early warning is less likely to be a false positive.

Example

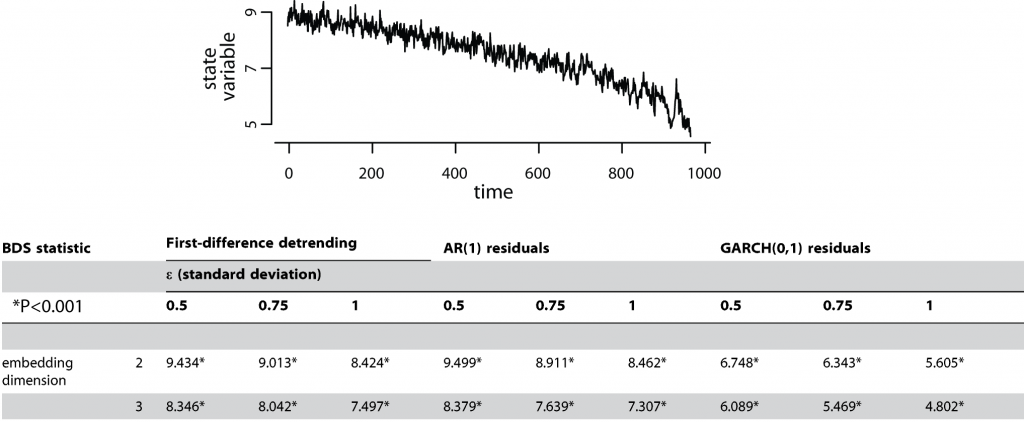
We present the BDS method applied to a simulated time series in which a critical transition is approaching (see panel below). We removed the underlying linear structure by: a. first-differencing, b. fitting an AR(1), or c. fitting a GARCH(0,1)) to the entire time series after log-transforming. The remaining residuals were used to estimate the BDS statistic for embedding dimensions 2 and 3, and ε values 0.5, 0.75, and 1 times the observed standard deviation of the time series (table). For each case, the significance of the BDS statistics was calculated using 1,000 bootstrap iterations. In general, the BDS statistic provided strong evidence for nonlinearity in the time series.

 

In principle, we can apply the BDS statistic within rolling windows to flag a potentially increasing nonlinearity in a time series that is approaching a transition. However, the fact that the BDS test requires a large number of observations for a reliable estimate and that it is sensitive to data preprocessing and filtering choices currently limits its use as a rolling window metric.